
БИБЛИОТЕЧНО
Формирование фондов: теория и практика
УДК 025.2.004.13
В. В. Нешитой
Статистическое моделирование библиотечного фонда
Цель статьи – разработка методов вычисления информационной полноты
комплектования библиотечного фонда, а также оценка его оптимального объёма на
базе статистических данных о количестве книговыдач и количестве выдач каждого
наименования документа.
Библиотечная статистика содержит разнообразную информацию, в том числе
всесторонне характеризующую библиотечный фонд. Для извлечения этой информации
необходимы математические модели, способные с высокой точностью аппроксимировать
(выравнивать) статистические закономерности. Рассмотрим некоторые из этих
моделей.
Кривые роста разных событий
В общем случае это кривые, которые описывают зависимости между количеством
произведенных испытаний и количеством наступивших при этом разных событий. В
качестве примеров можно привести такого рода зависимости между следующими
величинами:
- объёмом выборки в словоупотреблениях и объёмом словаря;
- количеством абоненто-запросов (т.е. запросов с учётом их повторяемости) и
количеством разных запросов;
- количеством книговыдач и количеством разных наименований выданных книг.
Кривые роста обладают общими свойствами: они выходят из начала координат под
углом 45 градусов, а с ростом числа испытаний тангенс угла наклона касательной к
кривой уменьшается, асимптотически приближаясь к нулю.
Имея статистические данные о количестве книговыдач х и количестве
разных наименований выданных книг у, можно построить кривую роста разных
выданных книг в зависимости от количества книговыдач. Эту статистическую
зависимость можно описать некоторой непрерывной кривой роста у=f(x)
(см., напр., [1]). Для этого необходимо выбрать наиболее подходящую
функцию и вычислить оценки параметров. Тогда вероятность выдачи новой книги,
т.е. не выдававшейся на запрос читателя от начала регистрации книговыдач, будет
равна первой производной от кривой роста [2. С. 53]
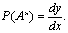 (1)
(1)
Следовательно, накопленная вероятность у выданных книг, т.е. функция
распределения F(y), будет равна разности
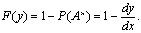 (2)
(2)
Функцию распределения (2) можно истолковать как вероятность удовлетворения
информационных потребностей пользователей, т.е. она может служить вероятностным
определением информационной полноты комплектования фонда объёмом у. Здесь
следует отметить, что общее число разных наименований выданных книг у со
временем растёт, поэтому полноту F(у) лучше назвать динамической,
или текущей полнотой. Формула (2) позволяет прогнозировать полноту
комплектования с ростом количества книговыдач х и числа разных
выданных книг у.
Ранговые распределения
Упорядочим все выдававшиеся книги, число которых равно у, по убыванию
(невозрастанию) числа их выдач за достаточно длительный период времени.
Подсчитаем общее количество книговыдач х. Вычислим относительную частоту
выдачи каждой книги с рангом r (рангом книги считается её порядковый
номер от начала частотного списка). Обозначим через pr относительную
частоту выдачи книги с рангом r. Эта частота является оценкой вероятности
выдачи данной книги. Итак, имеем

где mr –
абсолютная частота выдачи книги с рангом r.
Функция распределения в этом случае будет равна
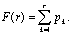
Она показывает, какая доля книговыдач приходится на первые r книг.
Статистическое ранговое распределение можно изобразить в виде графика
зависимости «ранг – частота». Однако такая форма представления никакой
новой информации не даёт, так как статистическая кривая (точнее, гистограмма)
резко убывает с ростом ранга и быстро приближается к горизонтальной оси.
Для более наглядного представления зависимости «ранг – частота» строят кривую
в двойном логарифмическом масштабе, т.е. «логарифм ранга – логарифм частоты». Но
такая кривая тоже несёт слишком мало информации о статистической структуре
фонда.
Чтобы извлечь максимум информации из статистических данных, необходимо
использовать другую форму представления ранговых распределений, которая вытекает
из теории обобщённых распределений автора [3. С. 139, 140].
Статистическое ранговое распределение необходимо представить в виде зависимости
«натуральный логарифм ранга – произведение ранга на относительную частоту», т.е.
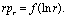 При
такой форме представления рангового распределения вместо убывающей кривой
получается обычная одновершинная кривая, которая даёт максимум информации о
статистической структуре фонда [4]: При
такой форме представления рангового распределения вместо убывающей кривой
получается обычная одновершинная кривая, которая даёт максимум информации о
статистической структуре фонда [4]:
если выборка однородная, то кривая распределения закономерно возрастает и
убывает;
если выборка неоднородная, то начало статистической кривой распределения
будет иметь резкие подъёмы и впадины. В этом случае можно выделить неоднородную
часть фонда (по частоте его использования). Эта часть находится левее последней
впадины перед закономерным ростом кривой;
в случае однородной выборки кривая распределения имеет одну моду (т.е. точку
на горизонтальной оси lnrC, в которой
произведение rpr максимально) и
две точки перегиба lnrA и lnrB, (т.е. точки, которые
отделяют выпуклую часть кривой от вогнутой). Эти точки примем в качестве границ
ядра фонда и зон рассеяния. При этом величина rA равна объёму ядра фонда;
rC – объёму ядра и первой зоны рассеяния; rB – объёму ядра и первых двух зон
рассеяния. Все остальные книги (с рангами r > rB) относятся к третьей зоне рассеяния.
Закон рассеяния книговыдач
Здесь уместно привести формулировку закона рассеяния журнальных публикаций
С. Бредфорда [5. С. 93]: «Если научные журналы расположить в порядке
убывания числа помещённых в них статей по какому-либо заданному предмету, то в
полученном списке можно выделить ядро журналов, посвящённых непосредственно
этому предмету, и несколько групп или зон, каждая из которых содержит столько же
статей, что и ядро. Тогда числа журналов в ядре и последующих зонах будут
относиться как 1: n: n2».
Однако из этой формулировки неясно, как вычисляются границы ядра и зон
рассеяния, сколько может быть этих зон, чему равна доля статей в каждой зоне.
Утверждение С. Бредфорда о том, что количество статей одинаково во всех зонах,
не соответствует действительности.
Для математически точного решения этих задач достаточно воспользоваться
обобщенными распределениями, в частности, второй системой непрерывных
распределений [3. С. 69]. Запишем первую обобщённую плотность этой
системы:
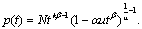 (3)
(3)
Здесь p(t) – плотность распределения; N –
нормирующий множитель;
 – параметры, которые для каждого
статистического распределения принимают свои конкретные значения и вычисляются
по статистическим данным. – параметры, которые для каждого
статистического распределения принимают свои конкретные значения и вычисляются
по статистическим данным.
Приведенная четырёхпараметрическая плотность распределения хорошо описывает
широкое разнообразие статистических распределений, в том числе ранговые
распределения периодических изданий, упорядоченных по убыванию числа помещённых
в них статей по некоторому заданному предмету, ранговые распределения книг и
т.д. Эта плотность является универсальным законом рассеяния публикаций [3.
С. 138-144], а также законом рассеяния книговыдач и т.д. Она позволяет вычислять
границы ядра и зон рассеяния. Из неё легко выводится математически точная
формулировка закона рассеяния в смысле С. Бредфорда, которая уточняет закон
С. Бредфорда. Эта плотность позволяет вычислять величину n, а также доли
статей в ядре и зонах рассеяния. Из этой плотности следует, что количество зон
рассеяния зависит от значений параметра u. Так, при u<1/2
существуют три зоны рассеяния, а при 1/2£ u<1 – только две
зоны рассеяния.
Графики плотности распределения (3), т.е. кривые распределения в зависимости
от значений параметров могут принимать различную форму. Например, при 0<kβ<1
кривая распределения является убывающей, т.е. она может описывать ранговые
распределения, а при kβ>1 кривая вначале растет, затем убывает. Площадь
под кривой распределения равна единице.
Преобразуем плотность (3) к другой форме, а именно: tp(t)=f(lnt).
Умножим левую и правую части на величину t, а величину
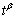 запишем в виде запишем в виде
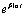 , что одно и то же. В результате такого
преобразования получим , что одно и то же. В результате такого
преобразования получим
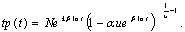
Последнее выражение также представляет собой обобщенную плотность. Она задает
первую систему непрерывных распределений и записывается в виде
 (4) (4)
где p(x)=tp(t), x=lnt.
Формула (4) может быть получена из формулы (3) традиционным путем – как
распределение функции случайного аргумента. Пусть x=lnt. Тогда
плотность p(x) можно найти по плотности p(t) с
помощью формулы
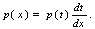 (5) (5)
Из равенства x=lnt имеем
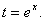 Тогда Тогда  а из формул (5) и (3) следует плотность
(4). а из формул (5) и (3) следует плотность
(4).
Приведенное преобразование распределений второй системы сводит их к
распределениям первой системы, т.е. плотность p(t) преобразуется к
плотности p(x). Кривые распределения, заданные плотностью (4), при
значениях параметра u<1/2 имеют моду xC и две точки
перегиба xA,
xB, которые расположены на равных расстояниях от моды. Эти
точки приняты автором в качестве границ ядра и зон рассеяния.
Таким образом, убывающая кривая рангового распределения, представленная в
виде зависимости
 не имеет никаких характерных точек, но
после ее приведения к форме не имеет никаких характерных точек, но
после ее приведения к форме
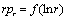 в случае однородной выборки она
превращается в одновершинную кривую, которая описывается обобщенной плотностью
p(x) и имеет моду и точки перегиба. в случае однородной выборки она
превращается в одновершинную кривую, которая описывается обобщенной плотностью
p(x) и имеет моду и точки перегиба.
Итак, для плотности p(x) имеем
хС – хА = хВ – хС
Учитывая взаимосвязи между первой и второй системами непрерывных
распределений, т.е. х = lnt, p(x) = tp(t),
для плотности p(t) можем записать
lntC – lntA = lntB – lntC
,
откуда следует равенство
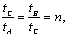 (6)
(6)
которое может быть принято в качестве закона рассеяния публикаций в смысле
Бредфорда.
Точки A, C, B делят все журналы в ранжированном ряду на
четыре части: ядро и три зоны рассеяния. Количество журналов, входящих в ядро,
определяется равенством tЯ = tА. Количество
журналов в первой зоне равно разности tI = tС - tА; во второй зоне tII
= tВ - tС. Остальные журналы относятся к
третьей зоне: tIII > tB. При этом количество журналов от
начала частотного списка до точки C в n раз больше количества
журналов в ядре. Количество журналов до точки B в n раз больше их
количества до точки С и в 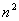 раз больше, чем в ядре. раз больше, чем в ядре.
Теперь можно дать математически точную формулировку закона рассеяния
публикаций. Она несколько отличается от формулировки Бредфорда (числа журналов в
ядре и последующих зонах относятся как 1 : n : n2).
Из формулы (6) следует, что между количеством наименований журналов от начала
частотного списка до точек A, С, В имеется соотношение
tA : tC
: tB = tA (1 : n : n2).(7)
В то же время между количеством наименований журналов в ядре и последующих
зонах имеется другое соотношение (при 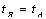 ) )
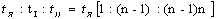 . (8) . (8)
Как видим, формулировка Бредфорда является комбинацией из двух точных формул
(7) и (8).
Обобщенная плотность p(t) дает возможность однозначно ответить
на вопросы, как определяется число журналов, образующих ядро, какая доля статей
содержится в нем, сколько может быть зон рассеяния, чему равна величина n.
Журналы, входящие в ядро, содержат долю статей, равную функции распределения
в точке A, т.е. F(tA). Аналогично доля
статей в журналах, входящих в ядро и первую зону рассеяния, составляет F(tC),
и т.д. Следовательно, доля статей в первой зоне рассеяния составляет F(tC)
– F(tA); во второй – F(tB) –
F(tC), а в третьей – 1 – F(tB).
Количество зон рассеяния, как правило, равно трем, но при определенных
значениях параметров аппроксимирующей плотности p(t) может быть
меньше.
На базе плотности p(t) нетрудно найти координаты трех
характерных точек и вычислить величину n. Абсциссы точек A и B
можно рассчитать при известных значениях величин tС
и n.
Мода tС находится из условия dtp(t)/dlnt =
0 и в общем случае для распределений I-V типов равна [3.
С. 141]
 (9) (9)
Величина n задается формулой
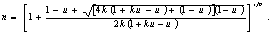 (10) (10)
Абсциссы точек перегиба вычисляются по формулам:
tА = tC /n; tB
= tC ∙n .
(11)
Формулы (6) – (11) являются следствием свойств обобщенной плотности
p(t). Они уточняют закон рассеяния публикаций Бредфорда, однако не
позволяют вычислять доли статей в каждой зоне.
Поскольку наиболее полной характеристикой случайной величины является ее
закон распределения, в данном случае рангового, то наиболее общий и
универсальный закон рассеяния публикаций – вторая система непрерывных
распределений, заданная тремя обобщенными плотностями [3. С. 142]. Первая
из них, т.е. плотность p(t) рассмотрена выше. Если по
статистическому ранговому распределению вычислен тип аппроксимирующей кривой и
найдены оценки параметров, то это значит, что установлен закон рассеяния
публикаций и на его основе могут быть вычислены все необходимые характеристики,
в том числе доли статей в каждой зоне.
Наилучшая аппроксимирующая кривая распределения для описания статистического
рангового распределения в общем случае вычисляется с помощью компьютерных
программ автора. Иногда можно ограничиться простыми моделями и методами оценки
параметров, не требующими сложных вычислений. Например, в некоторых
случаях статистическое ранговое распределение может быть достаточно точно
описано законом Вейбулла, который является частным случаем обобщённой плотности
(3) и следует из неё при k = 1,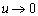 : :
  (12)
(12)
Функция распределения, т.е. интеграл от плотности (6) имеет вид
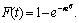 (13)
(13)
Чтобы проверить применимость закона Вейбулла для выравнивания статистического
распределения, функцию распределения (13) необходимо привести к форме прямой
 (14) (14)
Здесь величина t может обозначать ранг журнала или книги. Приняв далее
обозначения 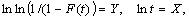 – получим уравнение прямой – получим уравнение прямой
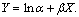 (15)
(15)
Вычислив по статистическому ранговому распределению логарифмы рангов 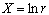 и значения величины и значения величины  , нетрудно построить график
зависимости (14) или (15). , нетрудно построить график
зависимости (14) или (15).
Если точки ложатся вдоль прямой, то закон Вейбулла может быть использован для
выравнивания статистического рангового распределения. Оценки его параметров
находятся по методу наименьших квадратов:
 (16) (16)
где  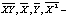 средние значения соответствующих
величин, которые вычисляются по статистическому распределению. средние значения соответствующих
величин, которые вычисляются по статистическому распределению.
При известных оценках параметров рассчитываются мода и точки перегиба кривой 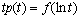 и величина и величина 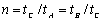 . Мода . Мода  находится из условия находится из условия 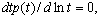 а точки перегиба – из условия а точки перегиба – из условия 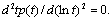
Рассмотрим известный пример рангового распределения журналов, публикующих
статьи по химии и химической технологии [5. С. 96].
В 10 850 журналах было обнаружено 187 911 статей по этой тематике. Накопленные
доли статей в t журналах частотного списка приведены в таблице (столбцы 1
и 2).
Рассеяние журнальных публикаций
по химии и химической технологии
|
Число
журналов,
в которых опубликованы статьи t
|
Доля статей
из опыта F(t)
|
Lnt = X
|
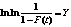
|
X * Y
|
X2
|
F(t)
по расчету
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
18
|
0,15
|
2,8904
|
-1,8170
|
–5,2519
|
8,3544
|
0,1537
|
|
50
|
0,25
|
3,9120
|
-1,2459
|
–4,8740
|
15,3037
|
0,2478
|
|
100
|
0,34
|
4,6052
|
-0,8782
|
–4,0447
|
21,2079
|
0,3358
|
|
500
|
0,62
|
6,2146
|
-0,0330
|
–0,2051
|
38,6213
|
0,6130
|
|
1000
|
0,75
|
6,9078
|
0,3266
|
2,2561
|
47,7177
|
0,7444
|
|
2000
|
0,85
|
7,6009
|
O,6403
|
4,8669
|
57,7737
|
0,8592
|
|
Сумма
|
–
|
32,1309
|
-3,0072
|
–7,2527
|
188,9787
|
–
|
|
Среднее = сумма/6
|
5,3552
|
-0,5012
|
–1,2088
|
31,4965
|
–
|
В этой же таблице дан расчет средних значений величин, необходимых для
вычисления оценок параметров закона Вейбулла по формулам (16). Они приведены в
нижней строке. Если по данным столбцов 3 и 4 построить график зависимости Y=f(X),
то эмпирические точки располагаются вдоль прямой [7]. Это значит, что в
качестве аппроксимирующего распределения правомерно использовать закон Вейбулла.
Вычислим оценки его параметров:
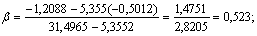 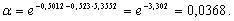
В столбце 7 даны расчетные значения функции распределения. Они мало
отличаются от эмпирических данных, которые приведены в столбце 2.
Итак, параметры закона Вейбулла для рассмотренного примера равны: α =
0.0368, β = 0.523. По этим параметрам вычисляются необходимые
характеристики:
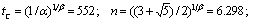

Приведенные здесь формулы для вычисления величин tC и n
получены из общих формул (9) и (10) при 
Значения функции распределения в трёх характерных точках равны (независимо от
значений параметров закона Вейбулла):
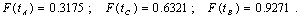
Это значит, что в ядро журналов (первые 88 журналов) входит 32%
статей по данному предмету (т.е. 59 660 статей). В ядро и первую зону рассеяния
– 63%, или 118 780 статей, а в ядро и первые две зоны рассеяния – 93%, или 174
212 статей. По зонам рассеяния доли статей распределяются так: первая зона
содержит 31% статей, вторая зона – 30% статей. На третью зону приходится лишь
7%, или 13 699 статей, хотя число журналов в этой зоне наибольшее и равно  , или 68% от общего числа журналов. Между
числом наименований журналов в ядре и последующих зонах справедливо общее
соотношение (8), которое с учётом величины n= 6,298
принимает вид , или 68% от общего числа журналов. Между
числом наименований журналов в ядре и последующих зонах справедливо общее
соотношение (8), которое с учётом величины n= 6,298
принимает вид
tЯ : tI : tII = tЯ(1
: 5.298 : 33.367).
Отсюда следует, что для более рационального комплектования фонда в него
следует включать те журналы, которые образуют ядро и первые две зоны рассеяния.
Количество таких журналов равно  , при этом полнота комплектования фонда , при этом полнота комплектования фонда 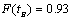 (в случае справедливости закона Вейбулла).
В общем случае она зависит как от вида закона распределения, так и от значений
его параметров, а в итоге – от статистических данных. Чтобы в нашем примере
повысить полноту комплектования фонда на 7%, пришлось бы увеличить его в 3,1
раза, т.е. на 7 334 журнала, что вряд ли (в случае справедливости закона Вейбулла).
В общем случае она зависит как от вида закона распределения, так и от значений
его параметров, а в итоге – от статистических данных. Чтобы в нашем примере
повысить полноту комплектования фонда на 7%, пришлось бы увеличить его в 3,1
раза, т.е. на 7 334 журнала, что вряд ли
целесообразно.
Величина 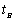 может характеризовать некоторый
оптимальный объём фонда с точки зрения информационной полноты комплектования.
Этот вывод можно распространить на другие виды изданий, например на книги. Тогда
величина tA будет обозначать ядро
книжного фонда (например, по некоторому тематическому разделу), а функция
распределения F(tA)– долю книговыдач, приходящуюся на
ядро книжного фонда. Величина tB даёт оценку оптимального
объёма фонда, а величина F(tB)– информационную полноту
комплектования фонда объёмом tB, т.е. вероятность
удовлетворения информационных потребностей пользователей этим фондом. В то же
время величина F(tB) – это доля
книговыдач, приходящаяся на фонд объёмом tB. может характеризовать некоторый
оптимальный объём фонда с точки зрения информационной полноты комплектования.
Этот вывод можно распространить на другие виды изданий, например на книги. Тогда
величина tA будет обозначать ядро
книжного фонда (например, по некоторому тематическому разделу), а функция
распределения F(tA)– долю книговыдач, приходящуюся на
ядро книжного фонда. Величина tB даёт оценку оптимального
объёма фонда, а величина F(tB)– информационную полноту
комплектования фонда объёмом tB, т.е. вероятность
удовлетворения информационных потребностей пользователей этим фондом. В то же
время величина F(tB) – это доля
книговыдач, приходящаяся на фонд объёмом tB.
При известных оценках параметров закона Вейбулла можно вычислить объём фонда
при заданной полноте его комплектования F(t):
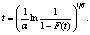
Итак, ранговый метод позволяет вычислять информационную полноту
комплектования фонда любого объёма, содержащего наиболее часто запрашиваемые
книги, решать обратную задачу – по заданной полноте вычислять необходимый объём
фонда, а также оценивать оптимальный объём фонда по точке перегиба B на
графике кривой  Для решения этих задач требуется
выполнять одно условие – учитывать количество выдач каждого наименования книги. Для решения этих задач требуется
выполнять одно условие – учитывать количество выдач каждого наименования книги.
Список источников
1. Нешитой В. В. Математические модели роста словаря и информационных
потоков / В. В. Нешитой // Учёные записки Тартуского гос. ун-та. – 1989. – Вып.
872. – С. 83–102.
2. Нешитой В. В. Исследование статистических закономерностей текста и
информационных потоков : диссертация … докт. техн. наук / В. В. Нешитой. –
Минск, 1987. – 505 с.
3. Нешитой В. В. Элементы теории обобщённых распределений : моногр. /
В. В. Нешитой. – Минск : РИВШ, 2009. –204 с.
4. Нешитой В. В. Форма представления ранговых распределений / В. В. Нешитой
// Учёные записки Тартуского гос. ун-та. – 1987. – Вып. 774. – С. 123–134.
5. Михайлов А. И. Основы информатики / А. И. Михайлов, А. И. Черный,
Р. С. Гиляревский. – Москва : Наука, 1968. – 756 с.
6. Нешитой В. В. Универсальные законы рассеяния и старения публикаций
// В. В. Нешитой // Веснік Беларус. дзярж. ун-та культуры і маст. – 2007. –№ 8.
– С. 128–133.
7. Нешитой В. В. Система непрерывных распределений в информатике и
лингвистике / В. В. Нешитой // НТИ. Сер. 2. – 1984. – № 3. – С. 1–6.
|
